Research
Research Highlights
Recent papers
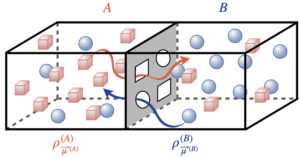
Thermodynamic systems typically conserve quantities ("charges") such as energy and particle number. The charges are often assumed implicitly to commute with each other. Yet quantum phenomena such as uncertainty relations rely on observables' failure to commute. This Perspective surveys key results in, opportunities for, and work adjacent to the quantum thermodynamics of noncommuting charges.
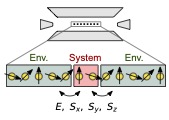
Noncommuting charges have recently emerged as a subfield at the intersection of quantum thermodynamics and quantum information. Until now, this subfield has remained theoretical. In this work we initiate the experimental testing of its predictions, with a trapped-ion simulator, We find that small subsystems equilibrate to near a recently predicted non-Abelian thermal state. This work bridges quantum many-body simulators to the quantum thermodynamics of noncommuting charges, whose predictions can now be tested.
In this paper we present a quantum algorithm for the dynamical simulation of time-dependent Hamiltonians. Our method involves expanding the interaction-picture Hamiltonian as a sum of generalized permutations, which leads to an integral-free Dyson series of the time-evolution operator. Our algorithm has a gate count that scales with an L1-norm-like scaling with respect only to the norm of the interaction Hamiltonian, rather than that of the total Hamiltonian. In addition, our algorithm retains the near optimal scaling with simulation error.
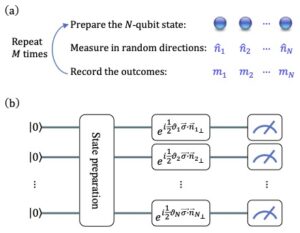
In this paper we introduce an approximate description of an N-qubit state, which contains sufficient information to estimate the expectation value of any observable to a precision that is upper bounded by the ratio of a suitably-defined seminorm of the observable to the square root of the number of the system's identical preparations M, with no explicit dependence on N. The operational procedure for constructing the approximate description of the state requires only single-qubit rotations followed by single-qubit measurements. We show that following this procedure, the cardinality of the resulting description of the state grows as 3MN.
Most cited papers
In this work we give semidefinite program (SDP) quantum solvers with an exponential speed-up over classical ones. We apply the SDP solver to the problem of learning a good description of a quantum state with respect to a set of measurements. The density matrix obtained is an approximation to the maximum entropy state consistent with the measurement data considered in Jaynes’ principle.
Characterizing complex quantum systems is a vital task in quantum information science. Quantum tomography, the standard tool used for this purpose, uses a well-designed measurement record to reconstruct quantum states and processes. It is, however, notoriously inefficient. In this paper we show that compressed sensing tomography of quantum systems is essentially guaranteed by a special property of quantum mechanics itself—that the mathematical objects that describe the system in quantum mechanics are matrices with non-negative eigenvalues. This result has important consequences on the efficiency of the data taking for quantum tomography, and enables us to construct informationally complete measurements that are robust to noise and modelling errors.
In this paper we generalize the concept of mutually unbiased bases (MUB) to measurements which are not necessarily described by rank one projectors. We derive their general form, and show that in a finite, d-dimensional Hilbert space, one can construct a complete set of mutually unbiased measurements (MUMs). Besides their intrinsic link to MUB, we show that these measurements' statistics provide complete information about the state of the system. Moreover, they capture the physical essence of unbiasedness, and in particular, they satisfy a non-trivial entropic uncertainty relation similar to MUB.
In this paper we introduce a fermion-to-qubit mapping defined on ternary trees, where any single Majorana operator on an n-mode fermionic system is mapped to a multi-qubit Pauli operator acting nontrivially on roughly log3(n) qubits. The mapping has a simple structure and is optimal in the sense that it is impossible to construct Pauli operators in any fermion-to-qubit mapping acting nontrivially on less than qubits on average.
Quick links

My papers
If you have any question on my papers (or on quantum, in general) please don't hesitate to contact me.